Не про химию
Introduction
Если бы я знал, что написание этого отчёта потребует столько же времени, сколько обрабока данных, я бы дважды задумался, прежде чем начинать вообще. Но дело начато, дело завершено, а потому написать надо.
Уф!
Во-первых, всем огромное спасибо.
Нет, правда. Действительно спасибо. Что столько людей согласятся участвовать в бессмысленных, на первый взгляд, расстановках температур кипения для веществ, о которых они впервые слышат -- это замечательно.
В чём был смысл этих действий?
Разумеется, вовсе не в том, чтобы оценить чьи-то познания в химии. А в том, чтобы получить ответы на несколько вопросов:
2. Можно ли, используя методы машинного обучения, свести эти оценки воедино?
3. Можно ли сделать эту оценку точнее, чем даёт простое усреднение результатов?
4. Можно ли её сделать точнее, чем точность самого сильного эксперта в группе?
6. Плюс кое-какие попутные наблюдения
Зачём всё это нужно?
Мне давно хочется создать систему для эффективного объединения разрозненных знаний группы людей в работающее целое. По возможности более эффективную, чем голосование. Способную приносить практическую пользу своим пользователям. Например, вырабатывая внятные модели происходящих в стране и мире процессов, основываясь на обрывочных пониманиях участников.
Однако это -- задача чудовищной сложности. И прежде, чем пытаться её понадкусать, неплохо бы потренировать зубы на родственной проблеме попроще. Ясно же, что если не удастся решить её, то и за более серьёзную браться нет смысла.
А что может быть проще, чем простая регрессия температур кипения, с одной-единственной выходной переменной, детально описанной в справочниках?
Вот так и родился этот эксперимент.
Перейдём же к его результатам.
Но сначала об участниках
Всего я разослал (через Bcc) 34 приглашения. Из этих тридцати четырёх:
-
4 человека (12%) ответили отказом
-
19 (57%) согласились поучаствовать
-
11 (33%) "затруднились с ответом"
Из согласившихся 19-ти в первом раунде ответили 13 человек (38% от числа приглашённых) и во втором 11 (33%). Меньше, чем я ожидал, но достаточно для набора статистики.
Ни одного профессионального химика среди ответивших не было. По роду занятий они разделились следующим образом:
-
Программисты: 8 человек
-
Медицинские работники: 2
-
Физики: 1
-
Домохозяйки: 1
-
Род занятий неизвестен (но не химия и не физика): 1
11 из 13-ти участников были мужчинами (хотя в приглашении их было 21 из 34-х).
Как выяснилось, могут, и зачастую на удивление приличые. Из 13 ответов девять статистически явно "экспертные", ещё три -- на грани случайности, и лишь один малоинформативный.
Задача стояла простая: поглядев на формулу и название химического вещества, "догадаться" о его температуре кипения.
Вот типичный график предсказанных температур против истинных:

Серый пунктир -- истинная зависимость. Красная черта -- линейная аппроксимация оценок, с розовой оценкой погрешности на уровне 98%.
Да, большинство цифр "мимо", да, наклон далёк от единицы, да есть "склонность к занижению". Но! Тенденция-то передана верно!
Обратите внимание на циферки в верхнем левом углу.
r - это величина корреляции по Пирсону. Грубо говоря, она показывает, какую долю изменения температуры кипения при переходе от одного вещества к другому отражают предсказания участника. 49% -- это очень неплохо.
А p -- вероятность получить такую же, или лучшую корреляцию, случайно разбросав точки по графику. p = 0.0074 демонстрирует, что, несмотря на серьёзные количественные промахи, оценки участника были отнюдь не "генератором случайных чисел" Это всё-таки именно экспертное мнение, пусть и с количественными погрешностями. Очевидно, у среднего образованного человека достаточно химической и физической интуиции, чтобы по названию и формуле вещества хотя бы грубо прикинуть его температуру кипения.
Лишь у одного из участников (№12) величина p составила 0.57 (и нет, это была не домохозяйка). Зная человека лично, я не думаю, что он отписался наугад. Скорее действительно "играл, но не угадал ни одной буквы":

Наилучший же результат показал участник №9 с фантастическим p = 2*10-12:

И нет, этот человек не химик и не физик. Просто, по его словам, помогло хождение на олимпиады в школьном возрасте и "не оценивать каждый пункт в отдельности, а делать это в сравнении <> сгруппировать газы, жидкости, и всё остальное и потом сравнивать их между собой <> на линейке температуры". Простой подход, а какой результат!
Полезно свести в таблицу параметры оценок всех участников:
| Участник | Средняя абсолютная ошибка в градусах Цельсия | Среднее трёх сильнейших ошибок в Цельсиях | p | Средняя абсолютная ошибка в логарифмах Кельвинов | Среднее трёх сильнейших ошибок в логарифмах Кельвинов |
| 9 | 45.8 | 185.0 | 2e-12 | 0.149 | 0.505 |
| 5 | 84.7 | 243.2 | 2.1e-6 | 0.258 | 0.558 |
| 1 | 70.5 | 343.2 | 3.4e-6 | 0.198 | 0.630 |
| 7 | 88.7 | 358.3 | 5e-6 | 0.243 | 0.743 |
| 11 | 101.0 | 297.8 | 2e-4 | 0.407 | 1.553 |
| 8 | 167.2 | 398.4 | 0.0074 | 1.152 | 3.917 |
| 3 | 159.7 | 464.3 | 0.018 | 0.923 | 4.064 |
| 4 | 181.8 | 1091.8 | 0.026 | 0.294 | 1.063 |
| 2 | 101.0 | 359.1 | 0.035 | 0.278 | 0.834 |
| 10 | 149.5 | 596.9 | 0.11 | 0.392 | 1.246 |
| 6 | 157.6 | 740.4 | 0.11 | 0.343 | 1.059 |
| 0 | 123.3 | 361.6 | 0.22 | 0.348 | 0.891 |
| 12 | 99.7 | 454.9 | 0.57 | 0.284 | 1.046 |
| Среднее | 117.7 | 445.8 | 0.405 | 1.393 |
Посмотреть на соответсвующие картинки можно здесь.
2. Можно ли, используя методы машинного обучения, свести эти оценки воедино?
Учитывая, что простое усреднение -- это частный случай линейной регрессии, а она -- частный случай многих более серьёзных алгоритмов, ответ очевидно положительный.
Но это теория. При проверке же на практике, несмотря на видимую простоту задачи, было оббито несколько углов. Об которые мы сейчас здесь и поговорим.
2.1. Обработка данных
Большинство методов как статистических, так и машинного обучения чувствительны к выбросам. Вплоть до того, что одна сильно "дурная точка" может сломать всё, если не принять мер.
Поэтому первое, что я сделал -- это обрезал выбросы. Температуры ниже -269 были установлены в -269, а выше +907 -- в +907. Да, указание в условиях температур кипения гелия и цинка было намёком на допустимый диапазон значений, но, видимо, намёк получился слишком туманным. Ибо были и +2000 для "страшного" CSe2, и, температуры ниже -300 для ряда газов. Я это отмечаю не ради похихикать, а скорее как характеристику разнообразия образований в таком, казалось бы, традиционном вопросе. Очень хотелось это разнообразие "запрячь в тележку", нежели вовлечь в спор.
Пропущенных данных почти не было. Там, где не удавалось получить их значения от участников, они заменялись средним по всем остальным участникам.
Затем все температуры были переведены в логарифмы кельвинов. Как ради большего физического смысла, так и чтобы дополнительно "сжать" данные, уменьшив влияние потенциальных выбросов. Отсюда и далее все действия, в том числе сравнение ошибок алгоритмов, велись в этой системе координат. Желающие взглянуть на свои оценки в ней приглашаются сюда.
А дальше -- классический supervised learning.
Вот у нас есть истинные значения параметра (Label), и есть оценки участников f0...f12, рассматриваемые как features:

От метода требуется, поглядев на эти данные, усвоить скрытую функциональную зависимость между меткой и фичами, и впоследствии использовать её для предсказания температур кипения ещё невиденных веществ только по оценкам участников.
Разумеется, здесь тоже есть тонкости.
Первый вопрос -- а какие алгоритмы участвовали в забеге?
1. Простое усреднение оценок всех участников. Я его оформил как "class AvgRegressor()" для единообразия интерфейсов. Разумеется, это весьма тупой регрессор, который на самом деле (почти) ничему не учится.
2. Несколько линейных регрессоров ElasticNet из sklearn.linear_model, с параметрами, выставленными, в общем, наугад.
3. RandomForestRegressor из sklearn.ensemble с 1000 деревьев, с критерием минимизации абсолютной средней ошибки ("mae"), а не её квадрата. Опять же, для вящей стабильности на малых и сильно зашумлённых данных.
4. StackingRegressor оттуда же, конечным регрессором которого был RandomForestRegressor, аналогичный вышеупомянутому, а двумя промежуточными -- два штуки ElasticNet, первый с высокой регуляризацией в L1, второй -- в L2.
Почему не нейронные сети? На хорошо затабулированных данных Random Forest выступает не хуже (а на малых задачах даже чуть лучше) нейронных сетей. Его процесс решения понятен человеку, в отличие от сетей. И, как и сети, он является универсальным аппроксиматором, то есть может описать любую зависимость.
Конечно, Random Forest не умеет сам создавать фичи. Кроме того, он хуже справляется с проблемами, в которых имеется нетривиальный "дальний" порядок между элементами данных ("лампочка" и "выключатель" на одной и той же картинке). Но в нашем случае всё это не нужно, поэтому Random Forest (или его близкие родственники вроде GradientBoostingRegressor) -- однозначно самый сильный аппроксиматор для данной задачи.
Есть у этого метода, однако, одна особенность, существенная для нашего случая. Random Forest не умеет экстраполировать за пределы увиденных им данных. То есть, если натренировать его на голубом участке вот такой проблемы, то за её пределами он выдаст оранжевую "полочку":
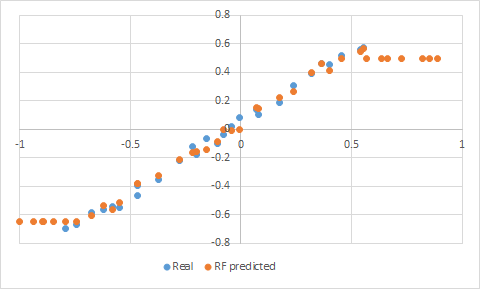
И эффект "полочки", к сожалению, может проявиться уже внутри знакомых данных при приближении к их краям, особенно, если плотность точек там невысока. Что приведёт к систематической ошибке для краевых данных. Иногда это несущественно, но у нас-то точек всего 29, и хочется получить максимально качественные предсказания для них для всех. Как с этим бороться?
Стандартный метод прост. Если вы знаете, что данные имеют тренд, надо его аппроксимировать ну вот хотя бы линейным регрессором, вычесть предсказания оного из данных, и затем накатить Random Forest поверх результатов. Собственно, StackingRegressor именно это и делает, за что и принят в команду.
Но в данном случае можно поступить проще и получить даже лучший результат. Перед тренировкой RandomForest-а я вычитаю из данных их среднее значение, взятое по включённым в тренировку участникам. А после предсказания это значение, разумеется, обратно к данным добавляется.
Про обучение и предсказание. Точек-то всего 29, как вообще можно на таком малом объёме оценить качество обучения и его ошибки?
Ответ -- в сочетании Cross Validation и Bootsrapping. Порядок действий такой:
1. Берём наши N = 29 точек и случайно исключаем из них k << 29 (обычно я брал k = 2)
2. Из оставшихся 29-k выборкой с повторением набираем случайно 29-k. То есть да, некоторые точки могут попасть в данные два и более раз. А некоторые не попасть вовсе. Классический bootstrapping.
3. Тренируем с нуля каждый из наших регрессоров (со всеми танцами про вычет среднего и т.п.) на выборке с предыдущего шага.
4. Натренировав, запрашиваем их предсказания для отложенных в сторону k = 2 точек.
5. Сравниваем предсказания с истиной, вычисляем для каждого абсолютную ошибку и запоминаем её (для каждого регрессора)
6. Повторяем цикл 1-5 эдак T = 512 раз.
7. Вычисляем среднее, средеквадратичный разброс σ и стандартную ошибку результата. Последняя, кстати, оценивается как ε = σ/√((N/k)-1). В знаменателе N, а не число тестов T, обратите внимание. Ибо количество информации в регрессоре фиксированно и определяется объёмом данных N. Громадное же количество тестов T потребно всего лишь для получения возможно более качественной оценки стандартного отклонения σ.
Это для оценки погрешности регрессоров. Для постоения графиков с "наилучшими" оценками для каждого из веществ повторяем то же самое, только вместо случайной выборки в п.1 последовательно перебираем все вещества по очереди, имея, эффективно, k = 1.
Вот так.
Что получилось? Об этом в следующем разделе.
3. Можно ли сделать эту оценку точнее, чем даёт простое усреднение результатов?
Да! Не очень, правда, намного, но да.
И это существенно. Простое усреднение -- это, фактически, голосование. То, что можно получить результат более точный, указывает, что по крайней мере для некоторых задач существуют лучшие способы построения правильного решения, нежели голосование.
Но к цифрам. Вот табличка, сравнивающая погрешности регрессоров на первом наборе данных:
| Regressor | Standard Error | Average of the worst three errors |
| Average | 0.226 ± 0.037 | 0.606 |
| E12 | 0.220 ± 0.034 | 0.566 |
| E21 | 0.237 ± 0.033 | 0.582 |
| E33 | 0.238 ± 0.036 | 0.597 |
| RF | 0.165 ± 0.026 | 0.407 |
| Stacking | 0.242 ± 0.037 | 0.581 |
(Ошибки выражены в логарифмах Кельвинов. Т.е., 0.2 означает ошибку от e-0.2 ≈ 0.82 до e0.2 ≈ 1.22 раз в Кельвинах)
Average -- это то, чего можно достигнуть простым усреднением по участникам. E12, E21, E33 -- различные линейные регрессоры. А RF -- это наш Rangom Forest. Побивший простое усреднение примерно в 1.4 раза.
Это, на самом деле, не сильно много. Я надеялся на лучший
результат. Не очень большая разница говорит о том, что большая часть
несогласия участников определялась всё-таки не различием их ментальных моделей
того, что и как кипит, а простыми шумами "с потолка". Ибо модели, даже взаимно
противоречивые, вычленить и свести воедино Random Forest
умеет, лишь бы они сами себе не противоречили. А вот шум предсказать
невозможно, и в общем случае нет лучшего метода для его устранения, чем
чуть более чем тупое аккуратное усреднение.
Занятно, что многослойный регрессор справился с задачей не лучше однослойного. Мы коснёмся ещё этой особенности.
А сейчас -- картинки. Предсказания против реальности для каждого из соединений, преобразованные для привычности обратно в Цельсии.
Сначала простое усреднение (голубая линия изображает собой истинную зависимость):
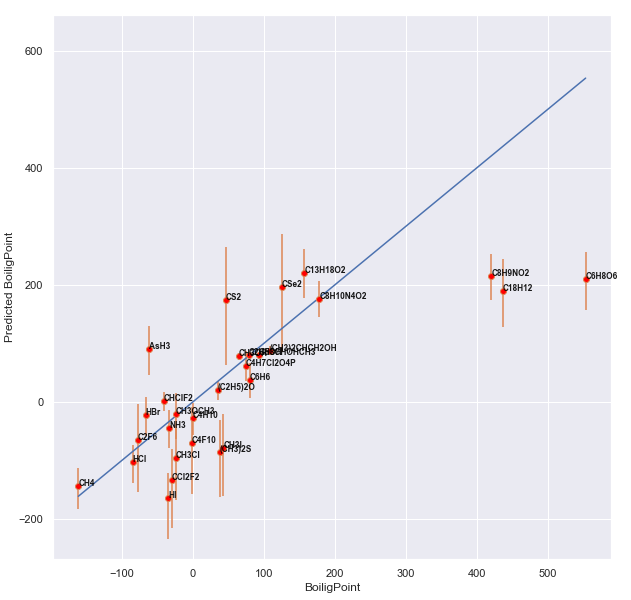
Random Forest:

Выглядит однозначно приятнее. Ещё раз отмечу, что ошибка сравнивалась в % погрешности в Кельвинах, так что метан CH4 слева и парацетамол C8H9NO2 справа -- это неточности примерно одного порядка.
4. Можно ли сделать оценку точнее, чем точность самого сильного эксперта в группе?
Вот тут начинаются тонкости. Мой наилучший ответ -- "иногда".
На первом наборе данных этого не случилось. Средняя ошибка самого лучшего эксперта составила 0.149, в то время как лучший машинный метод дал 0.165 ± 0.026. Вроде как хуже, хотя погрешность измерения допускает обратное.
В чём Random Forest смог побить лучшего эксперта -- так это в уменьшении трёх самых серьёзных ошибок. Для эксперта их среднее составило 0.505, а для машинного обучения -- 0.407.
Я пробовал выкидывать из данных самого сильного, самого сильного + самого слабого, половину самых слабых экспертов. Результат всякий раз оказывался одинаковым: предсказание с качеством на уровне самого сильного в выборке. В пределах погрешности.
По всей видимости, гипотеза о том, что основным элементом несогласия экспертов здесь был случайный шум, верна. И нужно вычерпать очень много этого шума, чтобы стать лучше лучшего из индивидуальных предсказателей. На первом наборе данных это сделать не удалось.
Но удалось на втором, и об этом сейчас будет подробнее.
Ответ -- "да, и с офигительной силой!"
Для этого эксперимента участники были случайно разделены на две группы. Первая (control) получила просто набор веществ для оценки, похожий на предыдущий.
Второй группе (treatment) были выданы истинные температуры кипения веществ в первом наборе, просьба с ними ознакомиться, плюс набор правил, помогающих в оценке.
Я надеялся хотя бы просто обнаружить хоть какой-то эффект от обучения экспертов. Результаты, однако, превзошли все ожидания:
| Параметр | Контрольная группа | Группа с обучением (treatment) |
| Средняя абсолютная ошибка в градусах Цельсия | 151.2 | 80.6 |
| Среднее трёх сильнейших ошибок в Цельсиях | 506.2 | 317.2 |
| Средняя абсолютная ошибка в логарифмах Кельвинов | 0.542 | 0.182 |
| Среднее трёх сильнейших ошибок в логарифмах Кельвинов | 1.640 | 0.520 |
| Средняя ошибка самого лучшего эксперта, в Цельсиях | 131.1 | 65.1 |
| Средняя ошибка самого лучшего эксперта, в логарифмах Кельвинов | 0.301 | 0.147 |
| Среднее трёх сильнейших ошибок лучшего эксперта, Цельсии | 527.5 | 308.8 |
| Среднее трёх сильнейших ошибок лучшего эксперта в логарифмах Кельвинов | 1.000 | 0.517 |
| Средняя ошибка предсказания, полученного методом усреднения | 0.372 ± 0.061 | 0.124 ± 0.023 |
| То же для RandomForest | 0.289 ± 0.051 | 0.133 ± 0.024 |
| То же для Stacking-регрессора | 0.292 ± 0.044 | 0.120 ± 0.020 |
Как видно, вторая группа (с обучением) обогнала первую по всем параметрам с колоссальным отрывом!
Что ещё любопытнее, регрессоры во второй группе показали результат существенно лучший (0.120 ± 0.020), чем оценка самого лучшего эксперта (0.147). Похоже, что обучение, устранив шумы, повысило внутреннюю когерентность моделей участников -- и тем самым дало возможность объединить их в нечто существенно более сильное. Многослойный регрессор, похоже, этим тут же воспользовался, чтобы слегка обогнать даже Random Forest.
Таким образом, можно считать доказанным, что при некотором (не сильно высоком) уровне обучения участников можно ответить положительно и на вопросы №4 и №5.
Но приведу ещё пару любопытных картинок.
Вот предсказания методом Random Forest для контрольной группы и для группы с обучением. Сначала контроль:
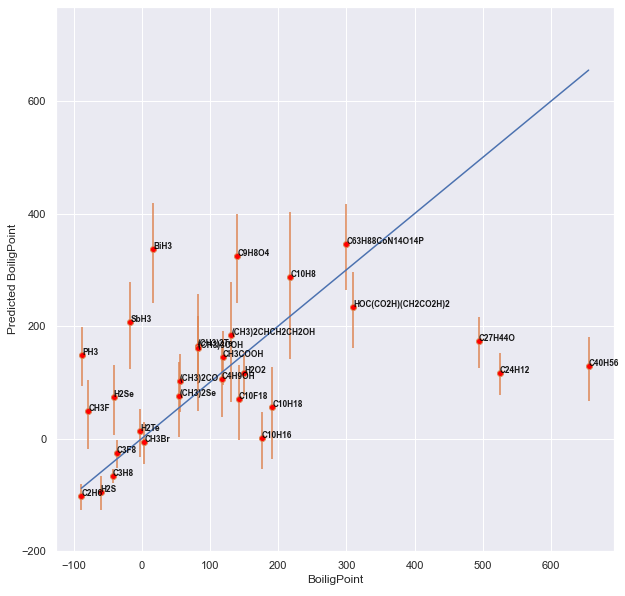
А вот группа с обучением:

Разница видна без всякой статистики!
Вот сравнение качества предсказаний участников до и после обучения. Пусть и на разных данных, столь значительные отличия явно говорят в пользу эффекта от обучения.
| Участник | p-value до обучения | p-value после |
| 0 | 0.22 | 0.0035 |
| 1 | 3.4e-6 | 1.2e-7 |
| 2 | 0.035 | 9.5e-9 |
| 4 | 0.026 | 7.8e-8 |
| 12 | 0.57 | 4.9e-8 |
В частности, у участника №12 p улучшился с малоотличимых от шума 0.57 до убийственного 4.9*10-8. Вон какая приятная картинка теперь:

Начнём с того, что во втором датасете я допустил опечатку. Для бромометана CH3Br я нарисовал в табличке структурную формулу бромоводорода HBr. Вот это:
![]()
Вместо правильного вот этого:
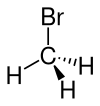
Однако никто не пожаловался, оценки были успешно выставлены и обработаны. Поэтому какое конкретно вещество имел в виду каждый из участников, видимо, останется уже тайной. Коан.
Ещё. Выданные участникам вещества можно отсортировать по средней ошибке, которую они допустили в оценке их температур кипения. Предположительно, чем выше ошибка, тем менее интуитивно понятно среднему участнику это вещество. Пользуясь этим методом, можно количественно охарактеризовать степень "эзотеричности" соединений для участников.
Отсортированные результаты для первого набора не особо удивляют:
| Формула | Название | Средняя ошибка, лог-Кельвины | Она же в процентах |
| C2H5OH | Этанол, этиловый (он же обычный) спирт | 0.015 | 1.50% |
| CH3CHOHCH3 | Изопропиловый спирт | 0.017 | 1.70% |
| CH3OH | Метиловый спирт, метанол | 0.017 | 1.73% |
| (CH3)2CHCH2OH | Изобутиловый спирт, 2-Метилпропанол-1, изобутанол | 0.020 | 2.02% |
| CHClF2 | Дифторхлорметан, фреон R-22 | 0.057 | 5.90% |
| (C2H5)2O | Диэтиловый эфир, он же просто эфир | 0.057 | 5.91% |
| C8H10N4O2 | Кофеин | 0.069 | 7.15% |
| C4H7Cl2O4P | Дихлофос, основной яд в одноимённом средстве от насекомых | 0.077 | 7.99% |
| C8H9NO2 | Парацетамол, ацетаминофен | 0.081 | 8.47% |
| C13H18O2 | Ибупрофен | 0.084 | 8.81% |
| C6H6 | Бензол | 0.096 | 10.05% |
| C6H8O6 | Аскорбиновая кислота, витамин C | 0.103 | 10.83% |
| C4H10 | Бутан, он же нормальный бутан, 1-бутан, неразветвлённый бутан | 0.111 | 11.74% |
| AsH3 | Арсин, гидрид мышьяка | 0.114 | 12.10% |
| C18H12 | Тетрацен, нафтацен | 0.126 | 13.44% |
| HBr | Бромоводород | 0.133 | 14.23% |
| NH3 | Аммиак, отвечает за запах нашатырного спирта | 0.144 | 15.49% |
| CH3OCH3 | Диметиловый эфир | 0.158 | 17.09% |
| HCl | Хророводород | 0.190 | 20.97% |
| CSe2 | Селенид углерода | 0.212 | 23.68% |
| CS2 | Сероуглерод, сульфид углерода | 0.222 | 24.88% |
| CH4 | Метан, главный компонент природного газа | 0.264 | 30.24% |
| CH3Cl | Хлорметан, метил хлорид, фреон R 40 | 0.338 | 40.25% |
| (CH3)2S | Диметилсульфид, тиобисметан, используется для придания мерзкого запаха природному газу | 0.343 | 40.92% |
| CH3I | Иодометан, метилиодид | 0.354 | 42.47% |
| C2F6 | Перфторэтан | 0.357 | 42.84% |
| C4F10 | Перфторбутан | 0.357 | 42.93% |
| CCl2F2 | Дихлордифторметан, фреон-1, фреон R-12 | 0.461 | 58.60% |
| HI | Иодоводород, иодистый водород | 0.495 | 64.12% |
Таки да, этиловый спирт C2H5OH -- самое знакомое народу вещество! Насмотря на индивидуальные ошибки, доходившие до 30-40 градусов, средняя ошибка составила всего 1.5%, т.е. 5 градусов.
Следом за этиловым плотной группой следуют ещё три спирта с весьма скромными ошибками.
Удивительным образом, родные братья фреон R-22 (CHClF2) и фреон R-12 (CCl2F2) заняли позиции почти в противоположных концах таблицы (5.9% и 59%). Я затрудняюсь это объяснить.
Наименее же знакомым для всех веществом, очевидно, оказался иодоводород HI, про свойства которого, похоже, вообще никто ничего не знал. Хотя в советском школьном учебнике химии про него вообще-то рассказывается (ухожу, ухожу, ухожу!)
Что ещё? Можно отсортировать участников не по их ошибке, а по количеству информации, которую Random Forest смог извлечь из их оценок для построения целостной картины. Это охарактиризует не столько точность представлений участников, сколько внутреннюю непротиворечивость оных (например, человек мог оценивать в Фаренгейтах, а не Цельсиях, или вообще поменять знак, но это были бы весьма информативные модели).
Для первого набора данных результаты оказались таковы:
| Участник | Вклад | ± |
| f9 | 0.371 | 0.0037 |
| f5 | 0.097 | 0.0016 |
| f3 | 0.084 | 0.0014 |
| f12 | 0.067 | 0.0010 |
| f10 | 0.062 | 0.0009 |
| f1 | 0.056 | 0.0008 |
| f7 | 0.055 | 0.0010 |
| f4 | 0.043 | 0.0007 |
| f2 | 0.038 | 0.0004 |
| f0 | 0.036 | 0.0005 |
| f6 | 0.034 | 0.0004 |
| f11 | 0.033 | 0.0003 |
| f8 | 0.025 | 0.0003 |
Участник №9 в одиночку дал больше трети всей информации для объединённой модели. Удивительно, но представления участника №12, несмотря на колоссальные абсолютные ошибки, оказались далеко не самыми малоинформативными, заняв четвёртое место в списке со своими 6.7% вклада.
7. Заключение
Показано, что как минимум в данной задаче вполне возможно сведение неточных, зашумлённых и малоинформативных предсказательных моделей группы людей в единую модель, обладающую большей предсказательной силой, чем и простое усреднение мнений участников, и чем мнение самого сильного эксперта в группе.
Качество объединённой модели, похоже, тем выше, чем умнее и образованнее участники. Грубо говоря (и определённо не имея в виду никого из присутствующих!), объединение мнений дилетантов порождает синтетического дилетанта, а объединение мнений экспертов, пусть даже резко друг с другом несогласных, имеет потенциал дать что-то более умное, чем каждый из экспертов по отдельности.
И ещё раз всем спасибо!
8. Данные (для желающих повторить и проверить)
Набор веществ первого тура (с температурами кипения).
Ответы участников первого тура.
Набор веществ второго тура (с температурами кипения).