
К вопросу об устойчивости эмоционального общения
Вместо предисловия
 |
| Неизвестно, кто первый открыл воду, но уж наверняка это сделали не рыбы |
Это не строгая научная работа. Отталкиваясь математическим шестом, под азартные вопли я перемахнул с десяток пропастей, по-хорошему требующих многолетнего выверенного возведения мостов -- и отнюдь не факт, что я всегда приземлялся на правильной стороне и не на четвереньки. Тем не менее, математика здорово помогает выразить концептуальный полёт интуиции, и именно в таком качестве я и прошу рассматривать её присутствие в данной работе.
О дивное сумасшествие 2006-2009 годов! Когда разрозненные сиэтловские тусовки вдруг обнаружили друг друга через Фейсбук. Будто изобрели межзвёздную связь и внезапно выяснилось, что мы не одни в этой Вселенной. Все ломанулись друг друга открывать, исследовать, искать новых друзей и подруг. Чем кончилась эта эпоха великих географических открытий? Мы не пьянствуем компаниями по 700 человек. Даже на ДроВАх.
Странным образом, самых лучших друзей мы не выбираем. Они вырастают из тех, кто рядом. Лучшие друзья детства -- это соседи и одноклассники. А соседи по общаге, распиханные случайно, с несовпадающими характерами, запертые на 2 года на 20 квадратных метрах, сплавляются так, что и 20 лет спустя не хотят расстаться.
Мы вовсе не "выбираем лучших". Ими
просто становятся
те, кто деятельно был рядом.
Наш сознательный выбор зачастую глупее нас. Близким стать может, по-видимому,
(почти) любой человек. Во всяком случае, куда более любой, чем привычно и
испуганно оценивает наше сознание. Избыток выбора убивает столь же верно, как и
его недостаток.
Безоговорочно принимая себя такими, какие мы есть, мы безнадёжно проигрываем.
Как и те, кто всегда гордо делают лишь то, что хотят. Они до конца жизни
обречены пить принёсённое с собой.
В угаре обдирания вишенок с тортов мы разучились читать людей в целом и решаем эту
проблему фокусировкой на отдельных буквах. Длине ног, величине IQ,
различимости дохода с 200 метров. Мы уже и пишем не словами, а этими самыми
буквами, отчего социальные сети превращаются в выставки "сверкающих, звенящих и
пылающих" повторов самого яркого иероглифа человека, давно уже не
складывающегося ни в какой ни смысл, ни образ...
Всё это имеет лишь интуитивное отношение к теме данной работе. Но очень нужно было это проговорить. Я же сказал -- вместо предисловия.
Итак,
Постановка задачи
Общение двух человек A и B на эмоциональном уровне можно рассмотреть как обмен сообщениями, представленными в виде векторов m, описывающих эмоциональное состояние отправителя:
- Зябко? И повел плечами. // m = <холод, любопытство, сочувствие>
-- Очень, -- ответил сосед с чрезвычайною готовностью, -- и, заметьте, это еще оттепель. Что ж, если бы мороз? Я даже не думал, что у нас так холодно. Отвык. // m = <холод, дружелюбие, желание поговорить, жалоба>
-- Из-за границы, что ль? // m = <любопытство>
-- Да, из Швейцарии. // m = <>
-- Фью! Эк ведь вас!.. // m = <изумление, лёгкое неодобрение>
Конечность длины этих векторов формально следует из возможности квантовомеханического описания человеческого мозга как ансамбля из ~1026 частиц. На практике длина достаточного описания, вероятно, существенно меньше и предположительно составляет не более ~4000 элементов, ибо именно этой цифрой характеризуется количество эмоций, различимых человеком [1].
Сообщения выражаются как словами, так и невербально -- их могут доносить позы, танец, выражение лица, одежда, комбинации этих вещей, равно как и отсутствие всяческой реакции.
Собака вертелась вокруг Лэха, поскуливая. Вдруг поднялась на задние лапы, оказавшись ростом с него самого, положила передние лапы ему на плечи, лизнула в нос. Он еле удержался на ногах. Отступил, наткнувшись на мобиль.
- Тутот просил узнать, может, вы ее возьмете.
- Взять?.. Как, совсем?
- Да. Хорошая ведь собака.
- ?..
- !..
- Ну пусть. Возьму.
В нашем мире всюду приходится делать упрощения и допущения:
Обмен сообщениями разделён по времени. Пока один отправляет, второй молчит. Что, конечно, не совсем так в реальности.
Партнёры детерминированы: на одинаковые сообщения отвечают одинаково. Что не кажется такой уж натяжкой при условии принятия следующих допущений.
Партнёры не меняются в ходе общения иначе как эмоционально.
Посторонние воздействия достаточно малы, чтобы их влиянием на общение собеседников можно было пренебречь.
Итак, общение начинается с того, что A отправляет сообщение m0 к B. Этот B получает послание, испытывает какие-то чувства и выражает их ответом m1 к A (тоже необязательно словесным). Таким образом A на своё послание m0 получает некое преобразованное сообщение m1. Это преобразование можно записать как результат воздействия некоторого оператора OB, свойственного человеку B, на полученное им сообщение:
m1 = OB * m0 (1)
Под умножением, разумеется, подразумевается действие оператора.
Корреспондент A, ощутив ответ, в свою очередь преобразует его собственным оператором OA, продолжая диалог сообщением m2 к B:
m2 = OA * m1 = OAOB * m0 (2)
Так происходит обмен эмоциональными сигналами. Очевидно, на шаге номер 2N получаемое корреспондентом A сообщение связано с исходным вот таким выражением:
m2N = (OAOB)N * m0 (3)
Удобно ввести оператор R (от слова relationship), описывающий взаимоотношения двух данных людей, как R = OAOB, и записать:
m2N = RN * m0 (4)
Очевидно, динамика чувств участников общения критически зависит от свойств созданного ими (совместно, хотя зачастую неосознаваемо) оператора R.
Данная работа исследует поведение эмоционального взаимодействия в зависимости от свойств оператора R.
Общие соображения
 |
| "...пред ними всякая птица лежит ощипанной!" |
Для начала отметим, что R непрерывен, что следует из общих физических соображений. Упрощённо, непрерывность значит, что результаты воздействия R на два бесконечно близких сообщения m и m' тоже бесконечно близки друг к другу. Действительно, если два сообщения отличаются настолько слабо, что разница между ними неуловима, то и отклики на них будут одинаковы.
R, представленный в виде матрицы, состоит только из действительных компонент, потому что обращает любой действительный вектор в действительный.
Наконец, R наверняка нелинеен -- как и всякий достаточно сложный природный оператор. И здесь возникает первый вопрос: а как бы выглядело общение, если бы он был линеен? И может ли это служить адекватной моделью реальности?
Линейный случай
Для подзабывших напоминаю, что линейность означает очень простое свойство: результат воздействия линейного оператора L на сумму любых двух векторов есть сумма результатов его воздействия на каждый вектор по отдельности:
L*(m1 + m2) = L*m1 + L*m2
"В быту" линейность может выражаться двумя способами. Во-первых, комбинированностью откликов:
Дано сообщение: "жена плачет и ухи просит". Сообщение разбивается на два: "жена плачет" + "жена просит ухи". Отклик на первое: "обнять и погладить". Отклик на второе: "налить ухи". Ответный отклик есть сумма индивидуальных: "обнять, погладить и дать тарелку ухи."
Нелинейным же ответом в данном случае было бы, например, сказать: "дорогая, при чём здесь уха, когда я купил тебе Мерседес!"
Второе проявление -- это когда отклик на скалярную компоненту сообщения пропорционален её величине:
Дано сообщение: "муж повысил голос в 2.5 раза". Отклик: "повысить голос тоже в 2.5 раза".
Итак, рассмотрим гипотетическое эмоциональное общение, описываемое строго линейным оператором отношений RL:
m2N = RLN * m0 (5)
В общем случае всякий линейный оператор RL обладает набором собственных функций фi и собственных чисел λi, таких, что:
RL * фi = λiфi (6)
и функции фi образуют полный ортогональный базис в пространстве действия оператора, который можно отнормировать.
Разложим начальное сообщение m0 по этому базису:
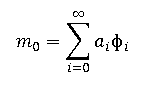 (7)
(7)
Суммирование прописано до бесконечности, подразумевая высокую размерность пространства. Но на самом деле, конечно, оно обрывается на каком-то высоком индексе, вряд ли выше нескольких тысяч.
Подставляя (7) в (5) с учётом (6), получаем:
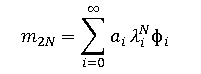 (8)
(8)
Как меняется "сила" этих сообщений с ростом N? Под "силой" будем понимать обыкновенную эвклидовую норму векторов, то есть скалярное произведение на своё сопряжение:
||m||2 = (m, m*) (9)
Учитывая, что базис {фi} ортонормирован, т.е. что (фi, фj) = δij, и подставляя (8) в (9), получаем:
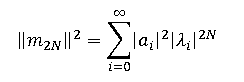 (10)
(10)
При больших N это выражение асимптотически ведёт себя как:
||m2N|| ~ |λmax|2N (11)
где λmax -- максимальное собственное число, имеющее ненулевой коэффициент разложения ai начального сообщения в базисе {фi}.
Это поведение, вообще говоря, нестабильно. Действительно, если |λmax| < 1, то норма ||m2N|| быстро стремится к нулю. Если |λmax| > 1, то она экспоненциально возрастает, что не может продолжаться бесконечно в силу ограниченности динамического диапазона человеческого восприятия (т.е. в общении что-то неизбежно "поломается" и оно станет нелинейным). Общение оказывается длительным только если |λmax| чрезвычайно близок к единице, что, как будет показано ниже, маловероятно.
Таким образом, следует вывод: участники, ограничивающие своё общение исключительно линейными откликами, (почти) неизбежно заканчивают его либо скандалом, либо молчанием, в котором "нечего сказать".
За какое время "разваливается" линейное общение? Если динамический диапазон амплитуд воспринимаемых человеком эмоций составляет D, и предполагая, что общение начинается где-то из его середины, то характерное количество итераций до выхода за пределы D либо полного затухания следует из (11) как:
Υ ≈ 1/4*Ln(D)/|Ln(|λmax|)| (12)
D для эмоциональной системы человека неизвестен. Однако вряд ли он на много порядков отличается от динамического диапазона более "простых" органов чувств, таких как зрение или слух -- ведь в конечном итоге все чувства трансформируются в сигналы нервной системы. Динамический диапазон нашего зрения составляет около 106 ([2]), слуха -- порядка 1010 ([3]). Примем 1010 как оценку сверху для эмоционального диапазона.
Величина |λmax| неизвестна и вряд ли кем-либо когда-либо количественно измерялась. Тем не менее, кое-что о ней понять можно, основываясь на достижениях матаппарата... ядерной физики. Дело в том, что если оператор RL устроен достаточно сложно, так что элементы его матрицы зависят от громадного количества самых разных факторов, то их в первом приближении можно описать как случайные. А распределение собственных чисел матрицы со случайными действительными элементами было получено ещё в 1960-е годы [4]. Этот результат утверждает, что у матриц достаточно большого размера n, заполненных нормально-распределёнными случайными действительными числами с дисперсией σ2, собственные числа стремятся к равномерному распределению по диску с центром в нуле и радиусом σ√n:
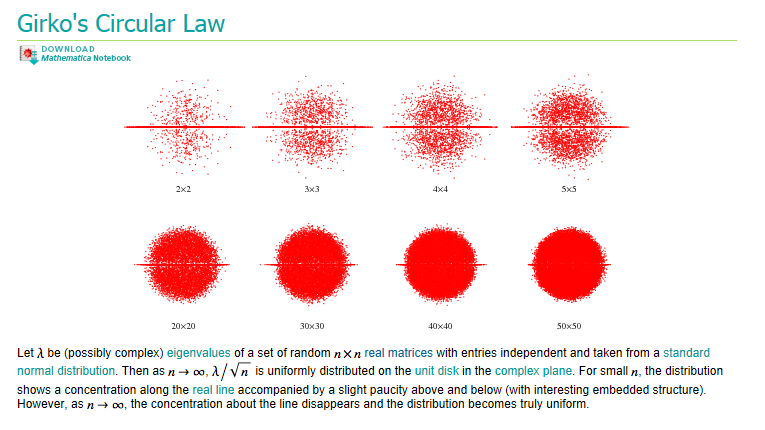
Даже небольшие матрицы недурно вписываются в этот закон. А в 1997-м удалось доказать, что это поведение сохраняется и для гораздо более широкого класса распределений, нежели гауссовое [5].
Таким образом, |λmax| ≈ σ√n. И хотя мы не знаем этих параметров, можно увидеть, что при "типичном" их выборе диапазон разброса их произведения может быть довольно широк. Так, эффективная размерность разговора n меняется, в зависимости от его темы, от ~1 (совсем простое эмоциональное содержимое) до как минимум десятка (сложные, многокомпонентые чувства), а гипотетически достигает, вероятно, нескольких тысяч. Параметр σ характеризует разброс "коэффициентов усиления" человеческих реакций на разные классы эмоционального воздействия, индивидуальные значения которых могут меняться от игнорирования (~10-3) до вспышки с жёстким ударом в морду за неудачное слово (~1015). Подобное разнообразие наводит на мысль, что вариация значений σ по матрице в целом между разными людьми и сценариями общения тоже составляет не менее нескольких раз.
Если возможный диапазон разброса величины σ√n покрывает как минимум порядок, то кажется маловероятным, что её значение (т.е. |λmax|) в каком-то конкретном случае будет очень близким к единице. Скорее всего, чаще оно будет либо существенно меньше, либо существенно больше. Иными словами, типично стоит ожидать |Ln(|λmax|)| >~1.
Подставляя это в (12), получаем оценку максимальной длины неразваливающегося общения, построенного исключительно на линейных откликах интеллектуально неизменных партнёров:
Υ ~ 6 (12.1)
Учитывая, что входные параметры входят в эту оценку под логарифмом, даже грубые ошибки в их значениях не приводят к радикальному изменению результата. То есть, (почти) любое "линейное" общение завершается за 3-10 обменов сигналами.
Это хорошо видно в общении профессионов на научные или аналогичные внятно очерченные темы. Такое общение очень линейно по своей природе (если в вопросе перечислено три пункта, то и ответ обычно выглядит как "1. ..., 2. ..., 3. ..., следовательно ..."). Дискуссии на таких форумах сходятся к истине или к признанному взаимному несогласию за полдюжины итераций. А вот флейм по природе своей нелинеен и способен порождать ветки с сотнями и тысячами комментариев. Легко :))
Линейные исключения
Итак, необходимым условием длительного и стабильного эмоционального общения партнёров с фиксированными реакциями является некоторая форма нелинейности оператора общения.
Может ли изменчивость партнёров вследствие общения заменить это условие? В рамках модели -- нет. Это показывается повторением предыдущих рассуждений с заменой m (вектора "эмоционального сообщения") на s, описывающего сообщение и эмоциональное состояние партнёров.
Контрпример, когда два идиота сидят и обмениваются сообщениями "один" -- "два" -- "три" -- "четыре" и так далее -- описывает общение, не являющееся ни линейным, ни достаточно многомерным с эмоциональной точки зрения для применимости вывода о спектре собственных чисел. Желающие могут убедиться в этом в качестве домашнего задания :)
Два наркомана играют в слова:
-- Москва-аа
-- Амстердам...
-- Москва-аа
-- Амстердам...
Исключения, вероятно, населяют области очень примитивного общения, затрагивающие единицы эмоциональных компонент. В этом случае распределение собственных чисел операторов отклика уже не описывается круговым законом и может получиться так, что все они окажутся на единичной комплексной окружности, описывая периодическое движение. Простейшим примером чего является занятие сексом :)
Далее, сила воздействия эмоций в значительной степени зависит от громкости речи. Регулируя её, можно прямо менять нормировку оператора RL и, таким образом, регулировать величину |λmax|, поддерживая некоторую устойчивость общения. Этот трюк работает лишь до тех пор, пока общение состоит преимущественно из компонент, имеющих явный и сознательно управляемый эквивалент громкости. Главным образом это голос, хотя некоторые таланты способны проделывать это с body language, выражением лица и даже CAPS LOCK-ом :)
 |
| Осьминог и человек -- братья навек. |
В целом, трудность здесь в том, что мы плохо умеем количественно измерять компоненты производимых нами эмоциональных впечатлений. Мы скорее только чувствуем их наличие. Причём малую часть. Большинство вообще пролетают мимо нашего сознательного восприятия. Собственно, тренировка актёра и состоит в том, чтобы учиться замечать и управлять как можно большим количеством этих компонент.
В этом наблюдается определённое сходство с осьминогами. Потенциальная сложность движения их щупалец настолько высока, что мощности мозга недостаточно для детального управления каждым по отдельности. Поэтому осьминог отдаёт щупальцам лишь общие указания ("схватить вот это!"), а конкретные нужные для этого изгибы рассчитываются нервными узлами "на местах". Так же и наши эмоции. В лучшем случае мы управляем лишь их общим ходом; детальные же движения, как правило, неподконтрольны сознанию и зачастую творят, черти, что хотят :))
Поэтому с точки зрения управления своими эмоциями правильным подходом является не заведомо обречённая попытка взять под контроль каждую из них, но нахождение неких "макросов" второго порядка, воздействующих на группы эмоций, сочетая и вычитая которые можно добиться более точных индивидуальных настроек. Как с кубиком Рубика, помните? Нет простого движения, переставляющего маленький кубик из угла в угол. Кубики сложно друг с другом сцеплены и ходят только группами. Но можно найти последовательность, перемещающую множество кубиков, которая, в итоге, достигает желаемого изменения, смещая попутно не слишком много посторонних кубиков.
К сожалению, рассмотрение этой задачи не входит в цели данной работы, а её решение, увы, далеко от завершения.
Нелинейные операторы и динамический хаос
Наконец, рассмотрим общий случай нелинейного отклика. Сложность данного класса взаимодействий радикально провосходит всё, что могут продемонстрировать линейные операторы. Это понятно хотя бы из того, что в нелинейном случае динамический хаос принципиально может возникать уже при скалярном m, например, в классической последовательности [6]:
xn+1 = r*xn*(1-xn) (13)
при достаточно больших r. В многомерном случае он возникает с ещё большей охотой, демонстрируя колоссальное многообразие страннейших решений, самым узнаваемым среди которых является, конечно, Аттрактор Лоренца:
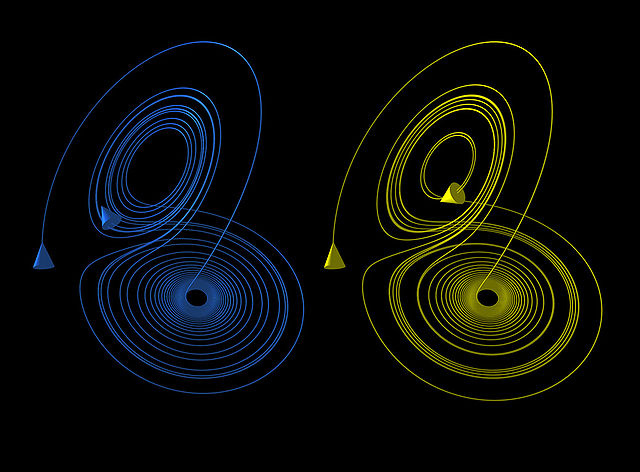
Динамический хаос -- штука очень интересная. Это когда система, управляемая вроде бы строгими и однозначными законами поведения, ведёт себя очень сложно и на внешний взгляд даже хаотически, не описываясь никаким очевидным простым приближением. Он "живёт" и никогда не зацикливается. Что ещё важнее, динамический хаос "ускользает" от всяких попыток его предсказать. С какой бы малой ошибкой ни было измерено начальное состояние такой системы, с каждым шагом эта ошибка будет в среднем расти, покуда не угробит всякую связь между реальным и рассчитанным состоянием.
Полный расчёт динамики системы вида (4) в случае нелинейного R выходит далеко за возможности современной математики. Однако некоторые частные случаи по-прежнему поддаются анализу, и мы этим с пользой займёмся.
Нелинейные операторы -- карта общения
Пусть в некоторый момент взаимодействие партнёров пришло к состоянию, когда по крайней мере один из них после каждого обмена сообщениями возвращается в эмоциональное состояние вблизи некой [вероятно, устраивающей его :)] фиксированной точки x. Отклонения от x в ходе общения невелики:
R*x = x + δx, где ||δx|| << ||x|| (15)
Рассмотрим следующую итерацию R*(x + δx). По аналогии с вектор-функцией n переменных от n аргументов, и полагаясь на непрерывность R, это выражение можно разложить в ряд по первому порядку малости:
R*(x + δx) ≈ R(x) + R'*δx = x + δx + R'*δx =x + Q*δx (16)
Здесь Q представляет собой матрицу, в позиции <i, j> которой стоит частная производная i-го компонента результата действия оператора R на x по j-ой компоненте вектора x, взятая в точке x, плюс единица по диагонали:
Qij = δij + (∂Ri/∂xj)|x (17)
Соответственно, динамика отклонения δx от фиксированной точки общения x приближённо описывается тогда уравнением:
δxN+2 = Q*δxN (18)
И оператор Q -- линеен! То есть, предыдущий результат о сходимости/расходимости линейного взаимодействие один в один переносится на данную задачу. Отсюда следует вывод, что всё пространство эмоциональных взаимодействий в общем случае разбивается на четыре класса зон:
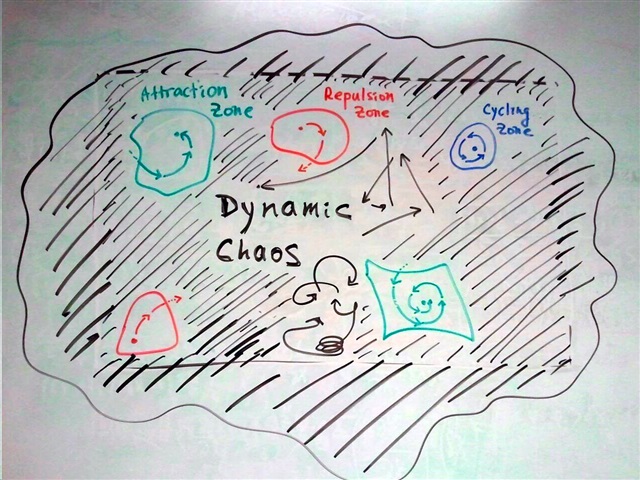
1. Зоны отталкивания (красные). Даже попав туда, общение их быстро покидает.
2. Зоны притяжения (зелёные). В них оба партнёра быстро (за 3-10 итераций) достигают устойчивого эмоционального состояния. Отметим, что это состояние может быть совсем не приятным для кого-то из них или даже для обоих. Всем, наверное, знакомо чувство взаимной холодности или неловкости, которое никак не удаётся разбить?
3. Редкие синие "зоны кружения", статистически более вероятные при общении, описываемом векторами с малым количеством компонент (секс, насилие, борьба двух очень сильных чувств).
4. И доминирующая над всем пространством область Динамического Хаоса, в честь Желязны окрашенная чёрным. Общение, угодившее в эту область, будет совершать самые странные, непредсказуемые, хаотические скачки, испытывать толчки и внезапные повороты. Оно будет искать новые точки равновесия, новые взгляды на собеседника, новые способы построения взаимодействия:
– У тебя нет книжек?
– Нет. Я несколько раз пытался сказать вам это, пока мы неслись в эту долбаную
рощу, но вы все время повторяли «Спокойно! Спокойно!», не слушая меня. Надеюсь,
теперь все спокойны?
– Я совсем не спокоен, приятель, – заявил тот, что был пассажиром. В его
зеркальных очках я увидел свое отражение. Оно мне не понравилось.
– Это идиотизм! – бросил я, перейдя на хинди. – Нестись неизвестно куда и зачем
со скоростью свихнувшегося бомбейского лихача, будто на нами гонятся копы!
Паспорта у меня припрятаны в этом вонючем отеле. Мне надо было убедиться, что вы
действительно те долбоебы, за которых себя выдаете. А теперь я убедился, что вы
действительно долбоебы и мозгов у вас не больше, чем у двух мух, совокупляющихся
на яйцах бродячего пса.
Они оба уставились на меня, подняв очки. Симптомы тяжелого похмелья на их лицах
растворились в улыбках.
– Где, черт побери, ты научился говорить так на хинди? – спросил водитель.
Оценка скорости сходимости в зоне притяжения (3-10 итераций) весьма важна с практической точки зрения. Если Вы видите, что вроде бы приближаетесь к желанному чувственному состоянию, но не достигаете его и через десяток-другой шагов, то это значит одно из трёх:
а) Вам только кажется. На самом деле Вы никуда не приближаетесь. Бросьте. Попробуйте достичь приятных Вам эмоций с другим человеком. Или с тем же, но иных :)
В частности, эмоциональная "химия" либо выстреливает от силы за десяток обменов впечатлениями, либо не выстреливает вовсе. Тут мне сейчас укажут на примеры, когда люди знали друг друга годами, а потом вдруг влюблялись и женились. Но это значит лишь, что они либо ни разу не оказывались в окрестностях точки притяжения (возможно, не пытаясь сблизиться), либо вдруг открывали ранее им незнакомые формы отношений ("спокойное счастье" вместо "безумной страсти"). Однако и в том, и в другом случае сходимость, если начинается, должна быть очень быстрой.
б) Что-то или кто-то воздействует на Вашего партнёра, "сбивая" его с курса. Может, шум. Может, усталость. Может, спешка. А может, оппонент, нагло шепчущий гадости о Вас и о вреде пива :) Смените время, место, обстановку, выкиньте оппонента, и попробуйте ещё раз. Об этом мы поговорим подробнее чуть позже.
в) Кто-то один или оба вы находитесь под властью буквально одной-двух сильнейших эмоций (ужаса, стыда, паники, страсти, гнева, тоски), водящих вас по кругу и не позволяющих толком почувствовать что-либо ещё. No comments, тут целый трактат можно написать об армиях, психологии толпы, стокгольмском синдроме и тому подобном.
Навигация в этом пространстве требует определить восемь действий:
| Область нахождения ↓ Желаемое действие → | Остаться в области | Покинуть область |
| Зона притяжения | Ничего не менять | Разрушить линейность | Дать задний ход | Усложнить общение |
| Зона отталкивания | Разрушить линейность | Дать задний ход | Усложнить общение | Ничего не менять |
| Зона вращения | Ничего не менять | Разрушить линейность | Усложнить общение |
| Зона хаоса | Разрушить линейность | Усложнить общение | Ничего не менять + терпение |
Кроме того, во всех случаях можно покинуть область, нарушив одно из основных ограничений модели -- отсутствие внешних воздействий. Но об этом позже, а пока поговорим про способы внесения нелинейности.
Первое, что приходит в голову -- намеренно случайные, бессмысленные действия. Данный оператор действительно нелинеен в каждом отдельном случае, но его усреднение на длительном интервале линейно. Особенно учитывая, что человек, на самом деле -- гораздо худший генератор случайных чисел, нежели нам хотелось бы думать. Так что не стоит этим злоупотреблять.
Неплохим нелинейным оператором является ответ только на превалирующий в сообщении стимул. Реагировать на самое яркое, остальное игнорировать. Правда, этот оператор не является непрерывным, и я не возьмусь предсказать результаты его применения даже в каких-то частных случаях.
Каков же общий вид простейшего нелинейного оператора? Следуя аналогии с разложением вектор-функции Rn -> Rn в ряд Тэйлора, k-ю компоненту результата воздействия такого оператора T на малый вектор δx можно записать как
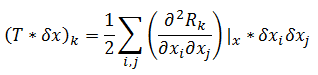 (20)
(20)
Тензор Tkij = (∂2Rk/∂xi∂xj) не обязан быть "плотным". Для возникновения нелинейности достаточно чтобы хотя бы один-единственный его элемент был ненулевым там, где не равны нулю компоненты сигнала за номерами i и j. Поэтому минималистский нелинейный оператор Θ приобретает вид:
Θ*x = ek*xi*xj (21)
где ek -- единичный вектор вдоль какой-то компоненты k (предположительно-желательно не совпадающей с i или j).
На человеческом языке его действие выглядит так: восприняв в сообщении две эмоции, ответить третьей, с силой, пропорциональной произведению двух первых. Чем сильнее ругается подруга и умоляет включить телевизор, тем быстрее надо ей поднести бокал вина :)
Гарантирует ли такой оператор возникновение динамического хаоса и, следовательно "вечную жизнь" отношений? Я не знаю. Но вижу, что он -- очень близкий родственник системы уравнений Росслера, гарантированно порождающей динамический хаос [8] при некоторых значениях констант:
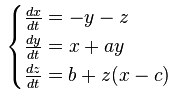 (22)
(22)
Аттрактор Лоренца [9] принадлежит к тому же семейству и тоже умеет срываться в хаос, используя всего три эмоциональных компоненты. Я, однако, не буду "переводить" эти уравнения в бытовые аналогии. Пусть это останется маленьким подарком для гиков в герметичной упаковке математической абстракции. Надо же создавать если не эволюционные преимущества, то хотя бы развлечения своему виду :) Нормальных людей прошу не обижаться. Вам это преимущество дано нахалаву, вы живёте эмоциональными контактами с самого рождения.
О внешнем воздействии
Примеров, когда описанная модель ни фига не работает, можно натыкать пальцем, не глядя, тысячами.
Люди десятилетиями живут в браке, борясь с нарастающим отталкиванием, покуда оно не разрывает дом и семью в пыльные клочья. Где здесь "десяток итераций"? Люди ухаживают за любимыми или ищут чьей-то дружбы годами -- получая иногда желаемое после сотен встреч. Мы вселяемся в общаги с чужаками, в которых бесит всё: задиристость в споре, выражение лица, привычка дрыхнуть по вечерам и разбросанные носки, а разъезжаемся через пять лет лучшими друзьями. Как так?
Ответ прост: люди непостоянны. Внешние воздействия их меняют, и куда больше, чем наши личные потуги. Почему отказ большинства людей нельзя считать окончательным, не услышав его примерно трижды? Да потому что одни и те же слова и улыбка дадут три разных результата в промозглом походе, в пропитаном ромом клубе, и в медитационной комнате. Нам нравится мыслить о себе как о чём-то постоянном, но человек -- куда больше тень внешних воздействий, нежели источник света. Integrity, часто ошибочно принимаемое за цель, а не средство, весьма невелико, и обитает более в сознании, нежели в наших чувствах.
Общение не описывается уравнением (1). Более близким к реальности будет вот это:
m1 = (OB + EB)* m0 (23)
Где EB -- оператор внешнего влияния на B. И раз на три наших запроса нужен один попутный внешний, то EB должен быть по воздействию как минимум не слабее OB. Карта отношений под его дуновениями плывёт и меняется ежеминутно, как тень листвы и пламя. Мы мыльная плёнка под ветром реальности. И где сегодня кружит водоворот притяжения, там завтра -- уже мешанина Хаоса, и непонятно, куда мчит новое течение:
Мы накапливаем эти изменения. Мы состоим из них.
Я, в 2008-м году написавший про себя 128 фактов, где он? 12 из этих фактов сегодня уже неверны, а ещё 14 изменились настолько, что стали неактуальны. Мы меняемся со скоростью, которую даже можно измерить: 10-9 Герц, или 3% в год. Именно столько себя мы теряем, заменяя на что-то другое, даже в спокойные периоды жизни. Не странно ли, что человек и живёт примерно 2*109 секунд?
Нет тех людей, что с визгом мчались когда-то по детскому саду. Нет милых одноклассниц, узнаваемых спустя 15 лет только по голосу. А встретив друга детства через 20 лет, я изумился, как же мало осталось у нас с ним одинаковых воспоминаний, и как много их набралось разных. У разных личностей -- разное прошлое, и неважно, что когда-то их предыдущие тела населяли вроде бы одну физическую реальность.
Обезьяна завоевала мир не своей силой, а взяв в лапу палку-копалку и острый камень. Взамен она перестала быть собой. Человек -- это прежде всего его инструменты, физические и интеллектуальные. Взяв обстановку и внешнее воздействие как инcтрумент, чего можно добиться? Чем можно стать, признав цвет, свет и микрофон частью себя самого?
И кто он тот "я", который всем этим управляет?
05.08.2013
Вопросы? Комментарии? В ЖЖ: http://eugenebo.livejournal.com/185576.html
===
Text Author(s): Eugene Bobukh === Web is volatile. Files are permanent. Get a copy: [PDF] [Zipped HTML] === Full list of texts: http://tung-sten.no-ip.com/Shelf/All.htm] === All texts as a Zip archive: http://tung-sten.no-ip.com/Shelf/All.zip] [mirror: https://1drv.ms/u/s!AhyC4Qz62r5BhO9Xopn1yxWMsxtaOQ?e=b1KSiI] === Contact the author: h o t m a i l (switch name and domain) e u g e n e b o (dot) c o m === Support the author: 1. PayPal to the address above; 2. BTC: 1DAptzi8J5qCaM45DueYXmAuiyGPG3pLbT; 3. ETH: 0xbDf6F8969674D05cb46ec75397a4F3B8581d8491; 4. LTC: LKtdnrau7Eb8wbRERasvJst6qGvTDPbHcN; 5. XRP: ranvPv13zqmUsQPgazwKkWCEaYecjYxN7z === Visit other outlets: Telegram channel http://t.me/eugeneboList, my site www.bobukh.com, Habr https://habr.com/ru/users/eugeneb0/posts/, Medium https://eugenebo.medium.com/, Wordpress http://eugenebo.wordpress.com/, LinkedIn https://www.linkedin.com/in/eugenebo, ЖЖ https://eugenebo.livejournal.com, Facebook https://www.facebook.com/EugeneBo, SteemIt https://steemit.com/@eugenebo, MSDN Blog https://docs.microsoft.com/en-us/archive/blogs/eugene_bobukh/ === License: Creative Commons BY-NC (no commercial use, retain this footer and attribute the author; otherwise, use as you want); === RSA Public Key Token: 33eda1770f509534. === Contact info relevant as of 7/15/2022.
===