Ну, может, и не вся наука, но по крайней мере физика и близкие к ней дисциплины.

"Странно" -- скажет читающий, -- "о каких проблемах с физикой вообще можно говорить? Успехи науки повсеместны. Рукой нельзя взмахнуть, чтобы не въехать локтем в какой-нибудь продукт высоких технологий. На исследования расходуются девятизначные суммы; революционные изменения в биологии, микроэлектронике идут с такой скоростью, что проморгаться не успеваешь. Что там опять курил автор?"

Не могу не согласиться: действительно, проникновение плодов науки в повседневность нынче сильно, как никогда. И в то же время мне кажется, что все эти инновации есть лишь инерция прогресса более раннего. А вместе с ними приходят и нарастают явления другого характера, весьма тревожного. В частности:

* Махровый расцвет псевдонауки. Начиная от относительно честных опровергателей ОТО, и кончая стопроцентным бредом, регулярно выплёскиваемым в миллионах экземпляров газетами типа "Комсомольской Правды". Собственно, я даже не могу припомнить, видел ли хоть одну связную и корректную статью о физике или родственных ей вещах в популярной прессе. Как минимум, что-нибудь переврут при пересказе. Как максимум, наплетут таких "торсионных полей", что и рыбу в эту газету страшно заворачивать :)

Хуже -- большинство людей сегодня не отличают порождений псевдонауки от науки. Инопланетяне для них такая же реальность, как черти и водяные для крестьян при Петре I. [Сие не значит, что я отрицаю возможность посещения Земли жителями иных звёзд. Но верить, что поход в соседний лес оканчивается насильственным полётом на Бетельгейзе???]

* Спад притока молодёжи в физику. Это характерно не только для России. В тех же Штатах точными науками интересуется хорошо если один школьник из класса. Остальные видят себя менеджерами, финансистами да баскетболистами. Неудивительно -- последние зарабатывают куда больше, чем профессора. В лучшем случае умные люди идут в программисты; но это, как мне думается, тоже ненадолго ввиду подступающего насыщения рынка.

* Трудности с пониманием. Помню, ехал я как-то домой в поезде, и попутчик мой поинтересовался, а чем это я занимаюсь на работе. Я раскрыл было рот... да так и заткнулся. Потому как понял, что это же потребуются все двое суток дороги, чтобы объяснить среднестатистическому россиянину с десятью классами проблему надтепловых электронов в плазме... При условии, что он будет всё это время меня внимательно слушать, а не пошлёт в ж%пу через пять минут.

Недавно встретил вот такой текст:

И, в то время, как, обливаясь потом, вы торжествуете свою победу и воображаете, что что-то такое сделали, что-то доказали противнику, в чём-то припёрли его к стене, -- он остаётся вполне спокойным, относясь более чем равнодушно к своему поражению. Стены, к которым его припёрли, для него -- из дыма.

Ужасно похоже на ощущения, возникающие, когда доказываешь какому-нибудь приверженцу Moon Conspiracy Theory бредовость его воззрений. Но тщетно. Его сознание полно совершенно мифических фактов, а способ мышления чужд нашей логике. Его не научили закону Паскаля и основам фотометрии; "стены" этих наук для него -- "из дыма", он спокойно проходит сквозь все противоречия и несёт свою чушь дальше, в массы таких же необразованных...

Цитата, кстати, принадлежит Павлу Флоренскому, весьма неглупому человеку, и возраст её на сегодня -- 100 лет. Но речь в ней идёт не о физике, а о споре христианина со "слабоверующими". Не правда ли, довольно неуютно испытывать те же ощущения сегодня, отстаивая базовые положения аналитических наук? Временами я даже ловлю себя на мысли, что пора внедрять методы святой инквизиции в борьбу с авторами всяких бредовых концепций... К счастью, приступы этой болезни обычно кратковременны и легко устраняются приёмом умеренных доз пива, так что ни одно животное, кроме меня, от этого не страдает.

Но если говорить серьёзно, то я полагаю, что какой-то кризис в современной науке всё-таки назревает. И что названные явления -- не разнородные случайности, "бывшие всегда", но первые признаки надвигающейся грозной проблемы, с которой современная наука (как социальный институт) столкнётся в полный рост в весьма обозримом будущем. Сейчас поясню подробнее...

...на пальцах

Для начала давайте взглянём на какую-нибудь область, наукой в традиционном понимании не являющуюся. Вот хоть на фотографию.

Опытный фотограф может знать ой как много. Физическую теорию процесса, три тысячи советов от профессионалов, плюс полмиллиона работ коллег, чтобы учиться на чужих ошибках. Но спросим: является ли всё это абсолютно необходимым, чтобы делать хорошие фотографии? Ответ очевиден: нет. Ну то есть да, с каждой отщёлканной плёнкой и прочитанной книжкой опыт фотографа растёт, и его фотографии становятся лучше. Но чтобы начать снимать, ничего этого ему не нужно. По большому счёту, ему даже всё равно, как там внутри работает фотоаппарат. А всё, что требуется -- это минимальное владение кнопками конкретной камеры и некоторый художественный вкус. Да, удачные снимки будут у него появляться, может, раз в сто реже, чем у профессионалов, но будут. А при одарённости минимальным воображением некоторые из этих кадров вполне могут понравиться и самым привередливым критикам. Немногие, но всё-таки.

А теперь представьте себе физика... или нет, пусть даже аспиранта, не умеющего пользоваться уравнениями Максвелла или брать интегралы. Что получится? Правильно. Приличный научный руководитель вышвырнет такого из вверенной ему части образовательного учреждения в ближайший же кол времени. В крайнем случае этому недоучке, может, доверят пожизненную должность лаборанта по мытью пробирок. Ни на какой больший вклад в науку такой аспирант рассчитывать не может.

Чувствуете разницу? Каждая дисциплина -- и физика, и фотография, и даже философия -- требует огромных знаний для того, чтобы достигнуть в ней совершенства. Но только у физики это знание имеет отчётливо выраженный пороговый характер. Для того, чтобы лишь начать физикой заниматься, нужно собрать багаж навыков, постигаемых не менее чем за несколько лет в приличном университете. Это включает полдюжины разделов математики, основные направления самой физики (механика, электродинамика и т.п.), основы эксперимента и, между прочим, ту же философию -- хотя бы для того, чтобы отличать её от науки :) И пока все эти знания не получены и не усвоены, человеку в физике делать нечего. Конечно, если речь идёт именно о физике как об исследовании природы, а не о применении её узких областей для изготовления винтиков [ничего не имею против индустрии, но просто это уже совсем другая область.]

В этом состоит основная особенность физики и близких ей наук -- в наличии своего рода "барьера" требований по знаниям к желающим хотя бы просто войти в клуб. Барьер этот высок, и он становится ещё выше, когда человек пытается открыть что-то новое. Ведь физика (как социальный институт) "не забывает" ранее сделанных открытий и не поощряет переоткрытий. Если какой-нибудь Вася Пупкин сегодня сядет и заново "с нуля" построит ОТО, никого это не впечатлит. Эйнштейн уже сделал это, и мы будем чтить за сей успех именно Эйнштейна, а не Васю Пупкина. Васе же, если он желает совершить аналогичную революцию, придётся сначала изучить работу Эйнштейна, а уж затем придумать что-то ещё более крутое. Например, внятную теорию квантовой гравитации.

Закономерность видна? Сегодняшнему Васе, чтобы продвинуть науку, мало быть умным, как Эйнштейн. Он должен быть умнее Эйнштейна!

Здесь люди начитанные могут сказать, что были в науке случаи, когда теории довольно крупные и солидные полностью отмирали и, таким образом, более не требовали изучения. Три классических примера -- это: а) геоцентрическая система мира Птолемея (весьма точно предсказывавшая видимые положения планет, кстати); б) теория флогистона; в) Томсоновская модель атома.

В ответ я соглашусь, что да, в истории науки действительно имели место подобные "революции". Но в данном тексте мы ограничимся рассмотрением тех (довольно крупных) интервалов в её развитии, когда подобных преобразований не было.

К тому же, даже такая серьёзная пертурбация, как "закрытие" флогистона, отменила всё-таки не всю физику, а лишь значительную её часть. Большая же часть новых открытий в физике не отменяла, но "включала в себя" концепции, известные ранее (явление, именуемое кумулятивностью).

Итак, что мы видим? Мы видим, что на пути каждого нового открытия сегодня стоит высокий барьер из сгенерированных ранее знаний, которые нужно усвоить, прежде чем бросаться в атаку на область. И, что самое интересное, с каждым новым открытием этот барьер становится всё выше. Ситуация чем-то напоминает прыжки с шестом, где каждый мировой рекорд задирает планку для тех, кто прыгает позже, на большую высоту.

Казалось бы, ну и что тут такого? Хочешь заниматься физикой -- иди в библиотеку, книжки читай. Как всё выучишь, возвращайся и поступай на общих основаниях. У нас все равны.

Проблема, однако, в том, что не все люди обладают одинаковыми способностями. Теоретически -- да, любой человек может изучить любую дисциплину. На практике вундеркинд сделает это за месяц, средний студент -- за год, а Жоре Офцоффу с его "room temperature IQ" в 84 единицы потребуется 300 лет. Поскольку люди столько не живут, это означает, на практике, что Жора Офцофф указанную область изучить не способен. Никогда. И физикой Жора Офцофф заниматься не будет, несмотря на всеобщее равенство. Барьер из минимального уровня знаний эффективно создаёт барьер по минимальному уровню способностей. И если способности человека находятся ниже этого минимума, он не может получить необходимого образования никогда, как бы сильно он того ни хотел. Точка.

Для физики уже сегодня уровень этого "порога" довольно высок, так что большая часть населения планеты его не преодолевает. Так, чтобы окончить приличный физфак, требуется IQ в области аналитического мышления никак не менее ~115. Таким интеллектом обладает лишь ~20% людей. И уж куда меньшая их доля наделена ещё более высокими IQ, потребными, чтобы усвоить крупную область современной физики и что-то в ней реально сделать.

Возникает интересная ситуация:

1. Развитие физики увеличивает количество минимально необходимых учёному знаний.

2. Рост объёмов знаний приводит к постоянному "задиранию" требований к будущим физикам.

3. Отсев становится жёстче, и приток новых кадров в науку уменьшается.

4. Доля физиков среди населения планеты падает.

5. Влияние физики на социальные явления и общее направление развития человечества сходит на нет. Физика превращается в узкоэлитарное знание, доступное 0.01% народа.

Фактически это -- своеобразная форма упирания в биологический предел интеллекта человечества. Не одного человека, а именно человечества в целом. Да, на индивидуальном уровне границ уму нет, ведь возможно рождение сколь угодно сильных гениев, способных решать сколь угодно сложные задачи. На практике, однако, "подходящих" гениев появляется столь мало, что они оказываются разрознены, не могут объединиться в эффективные социальные структуры, не способны объяснить свои идеи большинству и протолкнуть их в жизнь. Более того, я сильно подозреваю, что при слишком высоких способностях к аналитическому мышлению эти люди просто повреждаются в уме до того, как вырастут. От ежечасного столкновения с необоримым дебилизмом [с их точки зрения] окружающего общества :)

Я не знаю, имеет ли уже место вышеописанная проблема в современной физике, или нет. Но я чётко знаю, что если её развитие будет проходить по описанной схеме, то именно биологический предел человеческих способностей ограничит её рост, и случится это в обозримом будущем.

На сегодняшний день эффект "задирания планки" может частично компенсироваться экпоненциальным ростом населения планеты. Но даже это не устраняет проблему. Правда, чтобы понять это, придётся перейти к количественному описанию процесса.

В цифре

Попробуем рассмотреть динамику модели более строго. По сути, однако, в этом разделе будут лишь повторяться мысли из предыдущего, так что, если не интересно -- можете его прокрутить.

Итак, представим себе некую область познания или науки как p‑мерное пространство X (p, скорее всего, значительно больше единицы), где уже изученные участки отвечают заполненной области, а неизученные – пустой.

Считая, что заполнение этого пространства начинается с какого-то маленького знания («точечного прокола»), можно считать (с точностью до перенормировки координат), что изученный участок будет приблизительно отвечать некоей расширяющейся сфере в этом пространстве. Если принять такое описание, то можно вывести ряд интересных количественных соотношений.

Обозначим за x радиус "сферы познанного" [о единицах его измерения ниже], за S – общее число учёных, работающих или работавших в этой области [т.е. включая и уже умерших]. N пусть будет количеством людей, проживающих на Земле.

Предположим, что все земляне распределены по гауссиане относительно их способности заниматься дисциплиной X, если измерять её как результат "тестов на очки".

Это, кстати, скорее даже не предположение, а почти медицинский факт. Самые разные способности (сила, ум, красота), если выражать их в определённых единицах (обычно аддитивных: поднятый вес; количество решённых задач; количество сведённых с ума мужчин) дают именно гауссовое распределение.

Более того, когда речь идёт о науке, то значительной частью способностей к занятию ею является банальный IQ, который линейно пропорционален количеству решённых в тестах задач и имеет гауссовое распределение по самому своему построению.

Положим, что участие в X "защищёно" чётким порогом познаний -- то есть, что для каждого определенного момента времени существует некий минимальный уровень способностей к X, необходимый, чтобы успешно изучить и развивать эту область [это не противоречит тому, что люди обладают обучаемостью. Просто, как уже было сказано, при способностях ниже определённого уровня время обучения превосходит время жизни].

Если нам даны тесты на способности к X, дающие гауссово распределение результатов по набранным очкам, то единицы измерения x можно выбрать пропорциональными единицам теста. При таком выборе доля людей, способных успешно развивать область X, даётся хорошо известным интегралом:

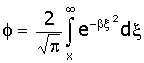                            (1),

где коэффициент b определяет ширину гауссовского «колокола» для людей в выбранной системе единиц.

В частности, если считать, что x -- это просто IQ, то b составляет что-то около 1/250.

Рассмотрим динамику числа учёных, занимающихся наукой X. Предполагая, что основным источником их притока является своего рода «вербовка» среди подрастающего поколения с последующих отсевом недостаточно способных, и что скорость этой вербовки пропорциональна как числу научных работников, так и числу всех людей, можно записать уравнение на изменение числа учёных S от времени:

                  (2),

где a отвечает за эффективность "агитации". Этя величина вероятно, переменна и зависит от общественного восприятия статуса науки, но для простоты мы положим её константой.

В эту формулу входят все физики, как ныне живые, так и уже нет. То есть, предполагается, что уже не живущие продолжают какую-то работу по «вербовке» через оставшиеся научные работы, публицистику, созданные школы, легендарную известность, наконец. Это, конечно, не совсем верно. Более точное выражение должно учитывать большую эффективность вербовки живыми через переменность a. Я, однако, сознательно завышу оценку эффективности, чтобы случайно не недооценить приток и количество научных работников.

Также предполагается, что общее количество участников движения X гораздо меньше числа всех живущих на Земле, дабы не возиться с эффектами второго порядка.

Наконец, в грубом приближении положим, что объём изученного пространства в X примерно пропорционален числу учёных, его заполняющих.

Это предположение более обосновано, нежели кажется с первого взгляда. В областях со слишком высокой плотностью научных работников наблюдается их повышенная «конкуренция», приводящая к «выталкиванию» более слабой их части в области менее перспективные и менее «населённые». Также, более сильные специалисты имеют тенденцию "отхватывать" части исследовательской работы у более слабых. Таким образом, на специалистов с одинаковыми интеллектуальными способностями в итоге приходится примерно одинаковый объём «их персонального» научного пространства, откуда можно заключить пропорциональность общего "объёма познанного" числу учёных:

      (3.2),

откуда

Наконец, будем считать, что общее количество людей на Земле растёт экспоненциально:

      (4)

с коэффициентом l примерно равным 0.03, если выражать время в годах.

На самом деле, в западных странах население почти не растёт и l = 0. Этот случай, как частный, будет рассмотрен отдельно.

Объединяя все вышеперечисленные выражения, получаем уравнение, описывающее динамику числа научных работников в рамках принятой модели: 

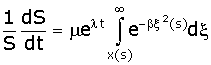        (5), где

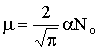
Аналитически это уравнение, скорее всего, не решается, но два частных (наиболее интересных) случая можно получить без особого труда:

1. Революционный прорыв, x очень мал. Это отвечает временам, когда новым направлением способен заниматься почти кто угодно ("Клондайк"). Решение для этого случая очевидно:

и описывает «взрывное» заполнение новооткрытой ниши (при l -> 0 сингулярности нет, а есть ).

2. "Зрелая" наука. Барьер x довольно велик, и интеграл (1) намного меньше единицы. Лишь немногие способны и далее продвигать свои направления. В этом случае (1) можно аппроксимировать асимптотическим разложением:

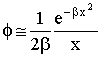          (1.1)

Подставляя его в (5), после ряда очевидных преобразований получим простое уравнение на x:

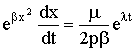  (6)

Приближённо решая его в предположении об асимптотическом разложении интеграла от экспоненты при больших x, получаем с логарифмической точностью, что:

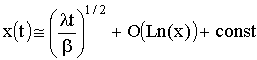   (7)

-- независмо от размерности заполняемого пространства! При этом, соответственно:

-- то есть, число учёных растёт как степенная функция, но отстаёт от роста населения (интуитивно очевидный результат).

 А их доля среди всех живущих подчиняется следующему закону:

то есть на больших временах доля научных работников в обществе экспоненциально убывает. Несмотря на свой ум и огромные способности, они постепенно теряют связи друг с другом и влияние на общество в силу своей малочисленности. Рано или поздно наступает момент, когда 99% населения перестаёт их понимать и замечать. Общество для учёных этой "эпохи" предстаёт конгломератом непробиваемых идиотов, не знающих элементарных вещей и до срыва голосов спорящих о бессмысленных или давно решённых вопросах.

Аналогичные выкладки для стран, население которых не растёт (Запад, Россия) дают вот такие результаты на "зрелой стадии" науки:

 ,

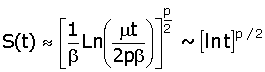-- то есть, хоть общее число физиков и растёт медленнее, их доля в составе населения спадает не так круто и общественное влияние сохраняется дольше.

Впрочем, принимать эти выкладки слишком всерьёз всё же не стоит. Точность их невелика хотя бы в силу упрощений использованной модели. Рассматривайте их скорее как некоторый полуколичественный анализ проблемы на чуть более формальном языке.

Безосновательные выводы и безответственные спекуляции

Попробуем разобраться, где же эта модель может быть неверна. Только, делая это, я немного смухлюю. Я буду допускать, что всё уже точно происходит, как описано, и смотреть, где и что должно случиться, чтобы кризис миновал. Соответственно, если модель неверна, то что-то из этого, возможно, будет иметь место уже сегодня; а если верна -- то мы узнаем один из вариантов будущего. Надеюсь, такое убийство двух зайцев одним кирпичом оправдает предлагаемый подход. Итак, поехали.

1. Мысль первая и наиболее очевидная: "автор, проверь арифметику!" Учитывая простоту вышеприведённых выкладок, кажется маловероятным, что я в них облажался; к тому же, описание явления "на пальцах" математику вообще не вовлекает. Тем не менее, если кто-то что-то заметит -- свистите :)

2. Обязательно ли изучение значительной части физики должно быть необходимым условием совершения фундаментальных открытий в ней? Можно ли успешно развивать науку без глубокого её знания? Могут ли, в принципе, дилетанты, не способные решать не то что дифференциальные, но и квадратные уравнения, вносить ценный вклад?

Эта мысль не столь бредова, как кажется. Собственно, именно такое "развитие вниз" испытывает в последние полвека программирование.

Вспомните самых первых программистов. Это были полноценные научные работники, плюс сильнейшие электронщики, и они писали всякие функции Бесселя прямо в машинных кодах. На перфокартах, в 200 байт памяти, желательно чтобы сразу без ошибок.

В 80-х, как я понимаю, появился класс "средних программистов". Им достаточно было хорошо знать основные алгоритмы и чётко владеть C или каким-нибудь Алголом. Знание "железа" уже обычно не требовалось.

В 2004-м требования к основной массе программеров упали до уровня 10-го класса хорошей школы. Библиотеки C# .NET делают за них быстрый поиск, сериализацию объектов, абстрагирование от железа и даже от самого языка благодаря help-ам, встроенным в Intellicence. Не говоря уже о том, что писать и отлаживать код в VS или Eclipse куда проще, чем в notepad-е или на перфокартах :)

Сие вовсе не означает, что не осталось сильных программистов. Знающие люди в этой индустрии есть, и они вполне способны кому угодно погнуть рога на тонкостях кэширования или там решений на сетках. Но их мало, и приличные компании за ними охотятся :) Основная же масса кода, особенно под Web, написана именно полуграмотными самоучками. Возможно это стало благодаря самим успехам программирования, переложившим большую часть работы человека на машины. В результате за полвека таких "обратных инвестиций" планка отбора не только не задралась, но даже сползла вниз, открыв потенциальный доступ в эту индустрию чуть ли не половине населения планеты.

Возможно ли что-то похожее с физикой именно за счёт развития "искусственного интеллекта"? Определённо да в некоторых областях. Так, научить человека простому численному интегрированию на C++ или Matlab куда проще, чем натаскать его в дифференциальных уравнениях; между тем первое умение эффективно заменяет второе во многих случаях. Другой пример: зачем разбираться в ТФКП для вычисления контурных интегралов, когда всё это пишется "левой ногой" на любом языке программирования? В общем, я не особо удивлюсь (хотя и не обрадуюсь), если эти дисциплины постепенно вытеснятся из программ многих ВУЗов.

Это однако, всё частные случаи. Если же напрячь фантазию, можно вообразить, что аналитические системы успешно возьмут на себя применение 90% знаний, получаемых сегодняшними физиками в университетах. Символьные преобразования? Уже написано. Решение задач университетского уровня по механике, электродинамике, термодинамике, квантовой механике? С натяжкой, но не так чтобы уж совсем невероятно. Зачатки наблюдаются. Проектирование физических установок? Этим уже сегодня пользуются, кто побогаче. Изучение 800 работ в области и поиск случайных, но ценных связей между ними (нынче -- работа экспертов)? Ждёт лишь момента, когда Google доиндексирует все книги из библиотек. В общем, не вижу никаких кардинальных препятстивий выходу "Microsoft Physicist 1.0 Beta" лет так через -дцать :)

Люди, пользующиеся такими системами, будут не менее эффективны во многих исследованиях, чем средний научный работник сегодня. При этом, однако, они будут от нас отличаться так же, как водители гоночных машин -- от их изготовителей. Совершенно иная профессия, с абсолютно другими требованиями к интеллекту, познаниям, и т.п. Даже в языке вряд ли у нас останется много общего...

Разумеется, "старые", традиционные физики-исследователи сохранятся. По дальним углам или по совсем уж недоступным вершинам чистейшей науки. Время от времени даже спускаясь на консультации и "прочистку мозгов" к физикам нового поколения. Но в целом они, подозреваю, останутся горсткой "староверцев"; и если кто-то из них и откроет что-то важное, у общества будут бо-оольшие трудности с тем, чтобы это понять или хотя бы заметить.

3. Вариант номер три -- что модель верна, но размерность пространства роста физики (p) настолько огромна, что возможно развитие почти любого направления почти независимо от остальных. При этом изученная область соответствует скорее не сфере, а этакому "ёжику" в дохренамерном пространстве, и описание с "планкой"  теряет предсказательную способность. Подобная модель, однако, кажется применимой скорее к искусству с его неисчислимыми вариациями жанров ("умеешь только рисом кидаться? Ну так начни писать картины из риса, и стань Эйнштейном в этом новом направлении!"). С современной физикой подобный номер всё-таки не проходит. Но как направление будущего развития это возможно, за счёт сваливания в сверхузкую специализацию. Скажем, человек 20 лет изучает поведение германия при криогенных температурах. А если при комнатных, или не германия, а галлия, то тут уже другие специалисты потребны. С таким же стажем. Плюс один "дилетант широкого профиля", который будет переводить слова эксперта по германию эксперту по галлию. Насколько эффективным будет прогресс при таком глубоком расщеплении? Не знаю.

4. Отмена строгого критерия истины. Когда работа принимается в науку, даже если она с высокой вероятностью неверна. Думаю, избрание этого направления грозит полным развалом науки как инструмента познания природы и улучшения жизни. Ведь если работа, позволяющая создавать новый пластик, столь же "ценна", как и ошибочная, то потребуются непомерные институты насильственной "политкорректности", со всеми вытекающими последствиями для любой возможности критического мышления... К сожалению, история показывает, что даже такие вещи, увы, случались -- вспомним лысенковщину. Более того, как раз-таки этим всё может закончиться, если модель верна -- ведь что толку в голосе одного знающего специалиста, когда его перекрикивают 200 невежественных "коллег"?

5. Отмена строгого критерия новизны. Работа принимается в науку, даже если она является практически плагиатом предыдущей. Либо за счёт того, что работ много и их всё равно никто не читал, либо от либерализации подхода: "в этом, кажется, что-то есть; не будем же спорить о вкусах". Хотя на первый взгляд подобная ситуация кажется немыслимой, она до определённой степени применяется в современной науке в области обучения студентов. Ведь даже хороший диплом бакалавра редко является открытием как таковым, но это никого не останавливает от принятия его автора в когорту "своих" (как продемонстрировавшего достаточное образование).

Между прочим, когда я писал свой магистерский диплом в 1999-м, со мной случилось нечто подобное. Решал я там одну задачку, вроде как даже на переднем крае науки, хоть и в пыльном углу, если честно... Разработал уравнения, её описывающие, а потом добил численно. И вот недели буквально за две до диплома занесло меня зачем-то в библиотеку. И совершенно случайно взял я там тонюсенькую брошюрку, препринт ИЯФ за 81-й, кажется, год. Гляжу -- а в ней русским по белому моя задача решена! Причём куда точнее и изящнее, чем это сделал я.

Меня, к частью, спасло то, что эта задача была всё-таки "сбоку" от основного направления работы, так что диплом я сделал нормальный. Но сам факт! Решение задачи оставалось погребено под ворохом других данных почти 20 лет. Согласно формуляру, книжку за всё это время брали 3 раза: в 81-м (сам автор -- видимо, проверить на опечатки); год спустя; и в 99-м, уже я. Всё.

Так что, кто знает, кто знает...

6. Успехи науки приведут к тому, что люди станут жить гораздо дольше, и любой дебил человек сможет, при желании, овладеть квантовой механикой на уровне Шрёдингера. Ну или мозг наш станет в 7 раз больше и в 10 раз быстродейственнее.

Хотя это и кажется идеальным выходом из возможного кризиса, на деле тут всё далеко не столь радужно. Дело в том, что мощные мозги нужны не только в науке. Поэтому другие формы человеческой деятельности сразу начнут конкурировать с физикой в борьбе за "двухголовую" молодёжь. И в какую сторону сместится равновесие, предсказать сегодня невозможно.

7. А не "подтянуть" ли нам школу?

Попасть струёй воды из шланга в куст легко может и пятилетний ребёнок. Между тем, сложность уравнений, описывающих гидродинамику струи, вполне достойна кандидатской диссертации. Но ребёнок прекрасно справляется с этой задачей не потому, что знает уравнения Навье-Стокса, а потому, что встречал воду, кусты и силу тяжести чуть ли не каждый день. Он набрался бессчётного множества впечатлений о поведении этих объектов и хорошо себе интуитивно представляет сценарии их взаимодействия.

Когда через 15 лет ему начинают вталкивать в голову понятие о магнитной гидродинамике, пространства для "интуитивного" усвоения материала уже не остаётся. Человеку приходится прибегать к аналогиям с уже знакомыми объектами -- например "напружиненному" шлангу как эквиваленту отрицательного магнитного давления. Аналогии эти слабы, часто неверны, и должны на каждом шагу подпираться костылями строгих уравнений. Скорость понимания и созидания получается черепашьей. Так, над проблемой удержания плазмы в магнитной ловушке люди бьются уже 50 лет. Между тем, я почти уверен, что если бы мы все с самого детства ежедневно видели плазму во всём многообразии её поведения, то эта проблема была бы для нас не сложнее задачи об "удержании" шампанского в бутылке.

Приведённый пример -- тоже аналогия, призванная прояснить мою мысль: а именно, мы, вероятно, очень много проигрываем на обучении детей в школах не тому и не так. Сегодняшняя школьная программа отстаёт от переднего края фундаментальных наук на десятки и сотни лет! Так, школьная математика ограничивается тем, что было известно ещё веке в 16-м [там, где дают основы интегрального исчисления -- в 17-м]; физика, за незначительными исключениями, остановилась на конце 19-го; химия местами доходит до середины 20-го. На этом фоне школьная астрономия выглядит ультрасовременной дисциплиной, рассказывая иногда об открытиях 10-20-летней давности :)

Должно ли нас удивлять потом, что между "хорошистом" современной школы и исследователем современных сверхпроводников лежит пропасть почти языковая? И что так мало людей в состоянии её преодолеть? Ой, вряд ли!

Можно ли эту пропасть уменьшить, радикально увеличив объёмы школьных курсов? При сегодняшних технологиях обучения и способностях людей -- нет. Доказательством тому большая доля "троечников", не справляющихся и с нынешней куцой программой. Если её раздуть, в их головах больше не осядет. Разве что лишь прибавится ненависти к обучению :)

Можно ли так перестроить школьную программу, чтобы при незначительном увеличении объёма насытить её понятиями и приёмами мышления из лучших ВУЗов? Я почти уверен, что да. Ведь такие вещи, как "множество", "функция", "интеграл", "N-мерное пространство", "ламинарный/турбулентный", "поле", "газ", "распределение" -- они вполне могут быть доступны "на пальцах" даже малому ребёнку! Пусть без формального доказательства, пусть с допущением некоторой фривольности, на уровне нестрогой интуиции, картинок. Но если целое поколение начнёт мыслить этим языком на бессознательном уровне, буря прорывов и новых открытий в самых трудных проблемах современной науки будет почти гарантирована. Просто потому, что этому поколению не надо будет "долго идти" до этих проблем; для них эти задачи могут оказаться столь же естественными, как для нас -- переливание воды из бутылки в стакан.

8. Объём познания в науке не пропорционален числу учёных, ею занимавшихся. Или пропорционален, но с сильно различающимися весами в разные моменты времени.

Заметим, однако, что линейная связь этих величин меняет динамику процесса, описываемого выражениями (8) и (9), лишь количественно. Качественный вывод об экспоненциальном убывании доли физиков в обществе остаётся верным при весьма широком спектре предполагаемых зависимостей S от х^p. Чтобы его разрушить, требуется чрезвычайно жёсткая зависимость типа

-- что соответствует такому заполнению пространства исследований, при котором на каждую мало-мальски различимую область науки приходится куча экспертов, и куча эта растёт быстрее, чем в разы, от каждого нового открытия. Интуитивно [:))] кажется, что это описание не похоже на ситуацию в науке, поэтому вряд ли описанная модель может быть неверна по причине допущения линейности.

9. Создание "новой" физики, которая всю массу знаний нынешней сможет выразить парой-тройкой простых и легко решаемых "уравнений".

Хотя я слабо верю в возможность существования подобной "новой" физики, совсем отвергать этот путь всё-таки не стоит. Некая возможность такого рода всегда есть.

Ведь можно годами разучивать свойства и правила применения 30 видов блоков, составимых из трёх-четырёх колёс и пары верёвок [я даже слышал, что в средневековых университетах этим занималась]. А можно усвоить законы Ньютона, малость алгебры и тригонометрии, и начать рассчитывать свойства этих и всех других блоков "с лёту".

Возможно ли что-то подобное с современной наукой? Открытие простого, единого "суперпринципа", из которого 50% людей будут в состоянии при необходимости вывести и уравнения Максвелла, и приближённое решение задачи N тел? Попытки построения альтернативного "суперпринципа" идут постоянно. Целая армия "непризнанных гениев" каждый год лепит новые теории относительности, электростатические космогонии, квантовые механики и домашние "термоядерные реакторы". Я видел некоторые из этих "работ" вблизи и даже общался с их авторами. Как правило, их "открытия" порождены невежеством, если не психопатологией. Но эти люди обычно движимы искренней жаждой познания, и нельзя совсем исключить, что в один момент какой-нибудь сумасшедший гений "проломит дверь" в таком месте, куда раньше попросту никто не заглядывал.

Скорее всего, это будет даже не гений, хотя человек определённо неглупый. Я вообще подозреваю, что многие революционные вещи открываются именно талантливыми недоучками. Не идиотами, которые не в силах понять даже основ старой школы; но и не истинными гениями, у которых будет хватать энергии, чтобы "грызть" в традиционном направлении даже тогда, когда все остальные отпадут без сил. А вот те, кто был в состоянии усвоить старое, но поленился "копать вперёд" и принялся ковырять стены по сторонам -- вот эти имеют небольшой шанс действительно найти новую дорогу.

Увидим ли мы что-либо подобное? Ждёт ли нас "закат физики"? Является ли всё вышенаписанное маразматическим бредом автора? К сожалению, "науке об этом... ничего не известно." Поживём -- увидим :)